Imagine a serene pond, its surface calm and reflective. On the first day, a single lily pad floats peacefully. It doubles in size every day. For the first few weeks, the change is barely noticeable. A few lily pads become a small cluster, but most of the pond remains open water. Then, suddenly, in the last few days, something astonishing happens. The pond, which seemed mostly empty just a short while ago, becomes almost entirely covered. This is the deceptive, yet powerful, nature of exponential growth.

This simple analogy, often attributed to Albert Bartlett, perfectly encapsulates the core concept of exponential growth: a process where the rate of growth itself is proportional to the current size or quantity. It means that the larger something gets, the faster it grows. What starts as a trickle quickly becomes a flood, often catching us by surprise.
Understanding the Basics: Linear vs. Exponential
To truly grasp exponential growth, it helps to contrast it with its more intuitive cousin: linear growth. In linear growth, a quantity increases by a fixed amount over a given period. Think of a savings account where you deposit a fixed amount every month, or a car traveling at a constant speed, covering the same distance each hour.
Exponential growth, however, is fundamentally different. Instead of adding a fixed amount, it multiplies the current quantity by a fixed factor. This compounding effect is what makes it so powerful and, at times, so difficult for our brains to intuitively comprehend. A classic example is compound interest, where your interest earns interest, leading to a much faster accumulation of wealth over time compared to simple interest.
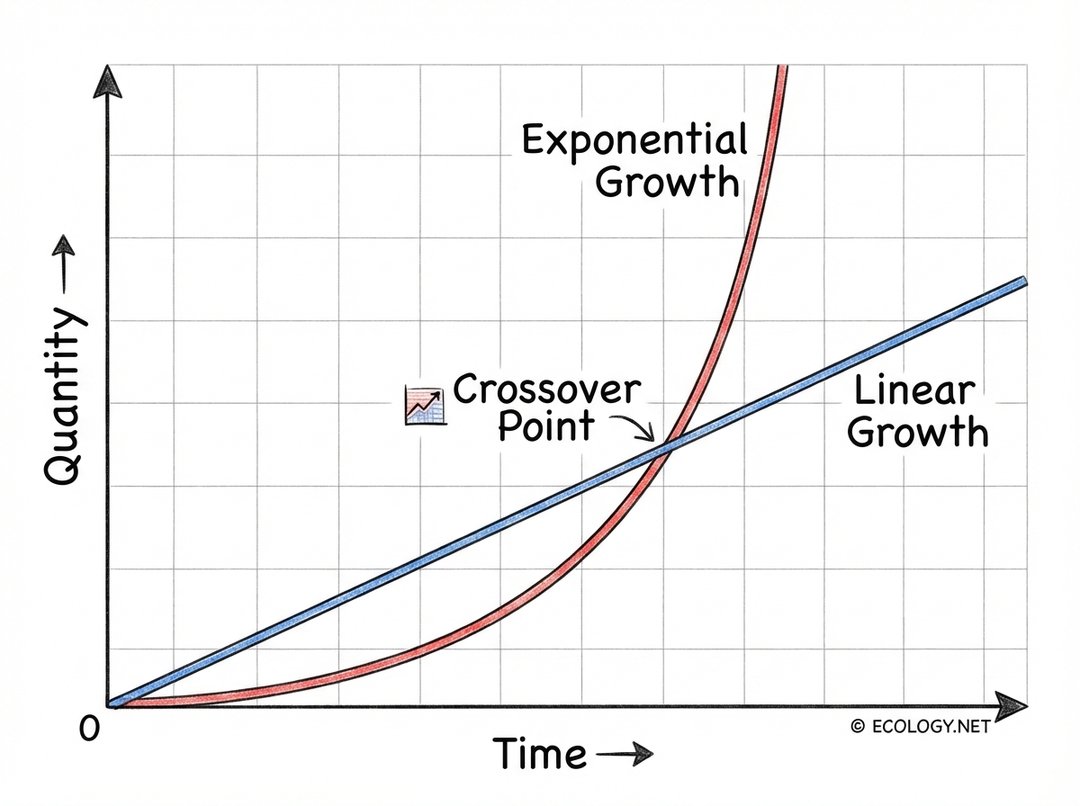
As the diagram illustrates, linear growth follows a straight line, steadily increasing. Exponential growth, on the other hand, starts slowly, almost imperceptibly, but then curves sharply upwards, eventually dwarfing any linear progression. This initial slowness is often what lulls us into a false sense of security, making the eventual rapid acceleration even more impactful.
The Doubling Time Phenomenon
A key characteristic of exponential growth is its “doubling time.” This is the time it takes for a quantity undergoing exponential growth to double in size. What is remarkable is that this doubling time remains constant. If a population doubles every 10 years, it will continue to double every 10 years, regardless of its current size. This means that going from 100 to 200 takes the same amount of time as going from 1,000,000 to 2,000,000.
Consider a bacterial colony that doubles every 20 minutes. If you start with one bacterium, after 20 minutes you have two. After 40 minutes, four. After an hour, eight. This seems manageable. But after just 10 hours, you would have over a billion bacteria. The growth in the last 20 minutes alone would be half a billion new bacteria, a number far greater than the total population after many hours of initial growth.
Exponential Growth in the Real World
The principles of exponential growth are not confined to theoretical ponds or petri dishes. They are fundamental to understanding many phenomena across various fields.
- Population Dynamics: In ecology, populations of organisms with abundant resources and no limiting factors often exhibit exponential growth. This is particularly true for species with high reproductive rates, like insects or bacteria, in new environments. Human population growth, for much of history, has also followed an exponential curve, though it is now showing signs of slowing in many regions.
- Disease Spread: The rapid spread of infectious diseases, especially in their early stages, is a classic example of exponential growth. Each infected individual can infect multiple others, leading to a rapid increase in cases until measures are taken or immunity develops.
- Technological Advancement: Moore’s Law, which posits that the number of transistors on a microchip doubles approximately every two years, is a famous example of exponential growth in technology. This has driven the incredible pace of innovation in computing and digital devices.
- Economic Growth and Finance: Compound interest, as mentioned, is a powerful financial application. Economic growth itself, when measured as a percentage increase year over year, can be considered exponential. Understanding this is crucial for long term financial planning and investment strategies.
- Resource Depletion: Conversely, the consumption of finite resources can also be viewed through an exponential lens. If consumption rates increase exponentially, resources deplete much faster than if consumption were linear, leading to critical shortages sooner than anticipated.
The Inevitable Limits: Carrying Capacity and Logistic Growth
While exponential growth is a powerful concept, it is crucial to remember that in the natural world, it cannot continue indefinitely. No population can grow without bounds forever. Eventually, limiting factors come into play, slowing the growth rate. This brings us to the concept of “carrying capacity.”
Carrying capacity (K) is the maximum population size of a biological species that can be sustained indefinitely by a given environment, given the available resources, habitat, food, and water.
As a population approaches its environment’s carrying capacity, resources become scarcer, competition increases, waste products accumulate, and predation or disease may become more prevalent. These “density dependent” factors cause the population’s growth rate to slow down. This transition from rapid exponential growth to a more stable, equilibrium state is described by “logistic growth.”
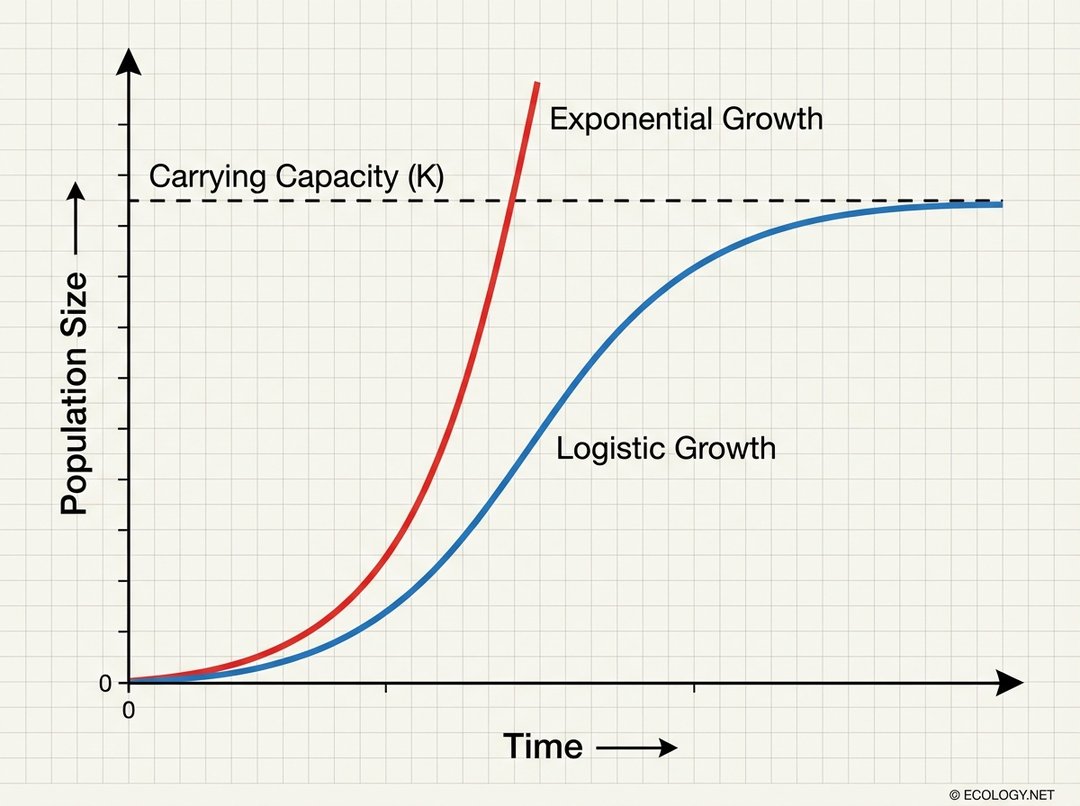
The logistic growth curve, often depicted as an S-shape, illustrates this process beautifully. It begins with a period of slow growth, followed by a phase of rapid, almost exponential acceleration. However, as the population nears the carrying capacity, the growth rate decelerates, eventually leveling off as the population stabilizes around K. At this point, birth rates and death rates become roughly equal, and the population size fluctuates around the carrying capacity.
Ecological and Societal Implications
Understanding the interplay between exponential growth and carrying capacity is fundamental to ecology and has profound implications for human society:
- Conservation Biology: Knowing the carrying capacity of an ecosystem for a particular species is vital for conservation efforts, preventing overpopulation that could lead to ecosystem collapse or underpopulation that threatens survival.
- Resource Management: Managing renewable resources like fisheries or forests requires careful consideration of their growth rates and the environment’s carrying capacity to ensure sustainable harvests.
- Urban Planning: Cities experience population growth, and understanding the exponential nature of this growth helps planners anticipate future needs for infrastructure, housing, and services.
- Environmental Sustainability: The exponential growth of human population and consumption patterns places immense pressure on Earth’s finite resources and natural systems. Recognizing this helps us understand the urgency of sustainable practices and resource conservation.
Conclusion: The Power of Understanding
Exponential growth is a force of nature, a mathematical marvel that shapes everything from the spread of a virus to the accumulation of wealth. Its deceptive initial slowness, followed by an explosive acceleration, often challenges our intuition. However, by understanding its mechanics, recognizing its presence in various phenomena, and appreciating the inevitable limits imposed by carrying capacity, we gain a powerful tool for predicting future trends, making informed decisions, and navigating the complexities of our world.
From the smallest bacterium to the global human population, the principles of exponential growth and logistic growth provide critical insights into how systems evolve and interact. Embracing this knowledge allows us to better manage our resources, mitigate risks, and build a more sustainable future.